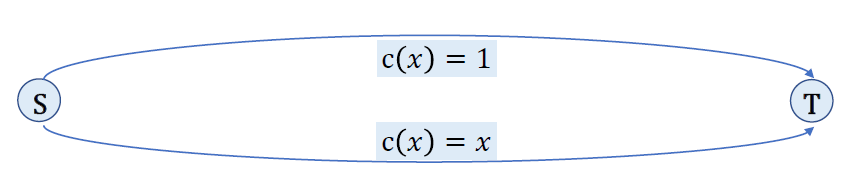原始对偶方法、整数规划

原始对偶方法

原始对偶方法的基本思路是利用前面讲过的互补松弛定理。

互补松弛定理：若 $x^*$ ， $y^*$ 分别是P、D的可行解，则： $x^*,y^*$ 最优 $\Leftrightarrow$ $\begin{aligned} (y^{*^T}A-c^T)x^*=0 \\ y^{*^T}(Ax^*-b)=0 \end{aligned}$ 。

所以，我们从D的一个可行解 $y$ 出发，尝试寻找P的可行解 $x$ ，使得 $x$ 、 $y$ 能够满足互补松弛条件。如果能够找到这样的 $x$ ，则 $x$ 、 $y$ 就分别是P、D的最优解；如果找不到这样的 $x$ ，说明 $y$ 还不是最优解，我们需要调整使之成为最优解。这个思路就是原始对偶方法。

判断最优解

考虑 （P） $\begin{aligned} \min \quad & c^Tx \\ \text{s.t.} \quad & Ax = b \\ & x \ge 0 \end{aligned}$ （D） $\begin{aligned} \max & \quad y^Tb \\ \text{s.t.} & \quad y^TA \le c^T \end{aligned}$

引入一个允许指标集 $J = \{\ j\ |\ y^TA_j = c_j\ \}$ ，由互补松弛条件可以看出，对于 $j \notin J$ ， $x_j = 0$ 。

设 $y$ 是D的一个可行解，则我们需要设法找到一个满足互补松弛条件的 $x$ ，也就是满足 $\left \{ \begin{array} {lr} Ax=b & \\ (A^Ty-c)^Tx=0 & \\ x \ge 0 & \end{array} \right.$ 。如果能找到这样的 $x$ ，我们就找到了P和D的解。

为了找到这个 $x$ ，我们E利用类似于两阶段法的思想：构造一个限制优化问题（RP）： $\begin{aligned} \min \quad &\sum\limits_{i=1}^m \bar{x}_i \\ \text{s.t.} \ & \displaystyle\sum\limits_{j\in J} a_{ij}x_j + \bar{x}_i = b_i \\ & x_j \ge 0,\ j \in J \\ & \bar{x}_i \ge 0 ,\ i = 1,\dots,m \end{aligned}$ 。如果RP的目标函数值可以取0，那么我们就找到了满足互补松弛条件的 $x$ 。

考虑原问题和其对偶问题取最优解时，目标函数值相同，我们写出RP的对偶问题（DRP）： $\begin{aligned} \max \quad & \tilde{y}^Tb \\ \text{s.t.} \quad & \tilde{y}^TA_j \le0,\ j \in J \\ & \tilde{y}_i \le 1, \ i = 1,\dots,m \end{aligned}$ 。设 $\tilde{y}$ 是其最优解。

若此时 $\tilde{y}^Tb = 0$ ，则 $y$ 就是D的最优解。否则， $\tilde{y}^Tb > 0$ ， $y$ 还不是D的最优解，我们需要改进 $y$ 。

改进解

我们取 $\hat{y}=y+\theta\tilde{y}$ 。其中 $\theta$ 是改进的步长， $\theta > 0$ 。 $\tilde{y}$ 是改进的方向。

首先考虑为什么这样结果是更好的： $\hat{y}^Tb = y^Tb + \theta\tilde{y}^Tb$ 。

因为 $\theta >0$ ， $\tilde{y}^Tb > 0$ ，所以 $\hat{y}^Tb > y^Tb$ ，D的目标函数值的确得到了改进。

然后考虑改进后能否满足D的条件： $\hat{y}^TA_j = y^TA_j + \theta\tilde{y}^TA_j$ 。

对于 $j \in J$ ，有 $y^TA_j = c_j$ ，又有 $\tilde{y}^TA_j \le0$ ，所以满足 $\hat{y}^TA_j \le c_j$ 。
对于 $j \notin J$ ，有 $y^TA_j < c_j$ ，因为此时是严格小于的关系，所以我们可以取到合适的 $\theta$ ，使得 $\hat{y}^TA_j $仍然满足 $\le c_j$ 的条件。

为了取到合适的 $\theta$ ，需要考虑 $\theta$ 的取值范围。由上面关于满足D条件的讨论，容易想到取 $\theta = \displaystyle\min\ \Bigg\{ \frac{c_j - y^TA_j}{\tilde{y}^TA_j}\Bigg\} > 0$ ，其中，需要满足 $j \not\in J,\ \tilde{y}^TA_j > 0$ 。这样就会让 $j \not\in J$ 中的一些限制变紧，其它限制则不会超过，仍然保证D可行。注意如果 $\theta$ 可以无限增大，说明对偶问题没有有限最优解，那么原问题无可行解。

由此我们将 $y$ 调整为 $\hat{y}$ ，得到新的允许指标集 $J$ 和 DRP，进入下一轮迭代调整，直到DRP的目标函数值取到0，此时 $y$ 就是D的最优解。

在最短路问题的应用

考虑有向图：，s 为起点，t 为终点，求 s 到 t 的最短路径。

得到点边关联矩阵 $A =$ $\begin{array}{c|ccccc} & e_1 & e_2 & e_3 & e_4 & e_5 \\ \hline s & 1 & 1 & 0 & 0 & 0 \\ t & 0 & 0 & 0 & -1 & -1 \\ u & -1 & 0 & 1 & 1 & 0 \\ v & 0 & -1 & -1 & 0 & 1\end{array}$ 。我们可以利用矩阵 $A$ 把 s 到 t 的最短路问题表示成线性规划问题。

设一条 s 到 t 的路径边集为 $P$ ，定义向量 $f = (f_1, \dots, f_m)^T$ ，其中 $f_i = \left\{\begin{array}{lr} 0, \quad e_i \notin P & \\ 1, \quad e_i \in P \end{array} \right.$ 。因为路径满足 s 的出度为1，t 的入度为1，其他途径点的入度等于出度，易知 $f$ 满足 $Af = (1, -1, 0, \dots, 0)^T$ ，其中1对应 s，-1对应 t。最短路是一条费用最小的s-t路 $P$ 。

因此我们可以写出如下初始线性规划（最短路的流模型）： $\begin{aligned} \min \quad & \displaystyle \sum \limits_{e\in E} c_ef_e \\ \text{s.t.} \quad & Af = (1, -1, 0, \dots, 0)^T \\ & f \ge 0 \end{aligned}$

可以想到，实际最短路问题中我们所求的最优解 $f$ 分量只有0和1两种取值，但在我们以往介绍的LP问题中，也可能产生小数解，会不会对此产生影响？实际上，在本问题中，求得的最优解一定是满足条件的。具体的证明会放在下一节整数规划中详细解释。

根据关联矩阵的性质，把矩阵 $A$ 的每一行加起来会得到零向量，所以 $A$ 中的行向量线性相关。不妨去掉 t 所在的一行，得到新的 $\bar{A}$ 以及最短路问题，并且能直接写出它的D形式与DRP形式：

（P） $\begin{aligned} \min \quad & \displaystyle \sum \limits_{e\in E} c_ef_e \\ \text{s.t.} \quad & \bar{A}f = (1, 0, \dots, 0)^T \\ & f \ge 0 \end{aligned}$

$\rightrightarrows$ （D） $\begin{aligned} \max \quad & \displaystyle y_s \\ \text{s.t.} \quad & y_i-y_j \le c_{ij}, \ (i,j)\in E \\ & y_t = 0 \end{aligned}$

$\rightrightarrows$ （DRP） $\begin{aligned} \max \quad & \displaystyle \tilde{y}_s \\ \text{s.t.} \quad & \tilde{y}_i-\tilde{y}_j \le 0, \ (i,j)\in J \\ & \tilde{y}_i \le 1 \ , i \in V \\ & \tilde{y}_t = 0 \end{aligned}$

其中，允许指标集 $J = \{\ (i,j)\ |\ y_i-y_j=c_{ij}\ \}$ ，D有一个明显的初始可行解 $y = 0$ 。

DRP问题的解是可以直接看出来的。

首先如果一条边在最短路径当中，则它对应的边 $f_e = 1$ ，则在D中对应的限制要取等号， $y_i-y_j=c_{ij}$ ，所以该边 $(i,j) \in J$ 。
其次，要让 $\tilde{y}_s$ 取最大值，如果没有 $\tilde{y}_t = 0$ 的条件影响， $\tilde{y}_s$ 最优解显然可以取到1。只有通过不断更新，增加 $J$ 中的边，直到某条边 $(i, t) \in J$ 时， $t$ 进入指标集中的边形成的连通块， $\tilde{y}_s$ 必须取0，此时我们也就找到了 s 到 t 的最短路。

对于改进解的过程，我们有： $\hat{y}_i=y_i+\theta\tilde{y}_i$ ， $\theta = \displaystyle\min\ \Bigg\{ \frac{c_{ij} - (y_i-y_j)}{\tilde{y}_i-\tilde{y}_j}\Bigg\} > 0$ ，其中 $(i,j) \notin J$ ， $\tilde{y}_i-\tilde{y}_j > 0$ 。

显然此时有 $\tilde{y}_i-\tilde{y}_j=1$ ，所以 $\theta = \displaystyle\min\ \{ c_{ij} - (y_i-y_j) \}$ 。所以 $\hat{y}_s = y_s + \theta$ 。

对于允许指标集 $J$ ，若 $(i,j) \in J$ ，有 $y_i-y_j=c_{ij}$ 。则 $\hat{y}_i-\hat{y}_j = y_i-y_j + \theta(\tilde{y}_i-\tilde{y}_j) = c_{ij}$ 。 $(i,j)$ 一旦进入 $J$ ，就不会再出来。说明该算法能够在 $O(M)$ 步内终止。

所以，原始对偶方法就是在不断扩展可到达 t 的顶点集，直到 s 进入该集合。

最短路问题例子

我们以下面的求 s 到 t 的最短路例子来演示原始对偶方法的应用。

$\rightrightarrows$ （D） $\begin{matrix} \max & y_s \\ \text{s.t.} & y_i - y_j \le c_{ij}, & (i,j) \in E\\ & y_t = 0 \end{matrix}$

D的初始可行解 $y = 0$ 。此时 $J = \varnothing$ ， $\tilde{y} = (1,1,1,1,1)^T$ 。取改进解， $\theta = c_{e7} = 2$ 。
改进后 $y = (2,2,2,2,2)^T$ 。此时 $J=\{e_7\}$ ， $\tilde{y} = (1,1,1,0,1)^T$ 。取改进解， $\theta = c_{e6} = 2$ 。
改进后 $y = (4,4,4,2,4)^T$ 。此时 $J=\{e_7,e_6\}$ ， $\tilde{y} = (1,1,1,0,0)^T$ 。取改进解， $\theta = c_{e5} = c_{e4} - 2 = 1$ 。
改进后 $y = (5,5,5,2,4)^T$ 。此时 $J=\{e_7,e_6,e_5,e_4\}$ ， $\tilde{y} = (1,0,0,0,0)^T$ 。取改进解， $\theta = c_{e2} = 1$ 。
改进后 $y = (6,5,5,2,4)^T$ 。此时 $J=\{e_7,e_6,e_5,e_4,e_2\}$ ， $\tilde{y} = (0,0,0,0,0)^T$ 。

所以最短路径长度 $y_s = 6$ ，路径为 $e_2 => e_5 => e_6 => e_7$ 。

整数规划

先从最简单的线性整数规划开始。

线性整数规划其实就是线性规划加上解必须为整数的限制，其基本形式为 $\begin{matrix} \max\limits_x & c^Tx \\ \text{s.t.} & Ax \le b \\ & x \in \mathbb{N} \end{matrix}$ 。我们之前见过的很多算法问题都能写成线性整数规划的形式，特别是能写成整数规划的一种特殊形式：0-1 规划。

0-1 背包问题

设共有 $n$ 件物品， $v_i$ 表示第 $i$ 件物品的价值， $w_i$ 表示第 $i$ 件物品的重量， $c$ 表示背包的最大承重， $x_i \in \{0, 1\}$ 表示是否选择第 $i$ 件物品。那么 0-1 背包问题可以写为 $\begin{matrix} \max\limits_x & \sum\limits_{i=1}^n v_ix_i \\ \text{s.t.} & \sum\limits_{i=1}^n w_ix_i \le c \\ & x_i \in \{0, 1\} \end{matrix}$

最小生成树

设共有 $n$ 个点，点集为 $V$ ， $(i, j) \in E$ 表示从第 $i$ 个点连到第 $j$ 个点的一条有向边（一条无向边就相当于两条有向边）， $w_{i, j}$ 表示边权， $x_{i, j} \in \{0, 1\}$ 表示这一条边是否在最小生成树内。那么最小生成树问题可以写为 $\begin{matrix} \min\limits_x & \sum\limits_{(i, j) \in E} w_{i, j}x_{i, j} \\ \text{s.t.} & \sum\limits_{(i, j) \in E} x_{i, j} = n-1 \\ & \sum\limits_{i \in S, j \not\in S} x_{i, j} \ge 1 & \forall S \subsetneqq V \\ & x_{i, j} \in \{0, 1\} \end{matrix}$

第一项限制保证了生成树中有且仅有 $n-1$ 条边，第二项限制保证了生成树的连通性。因为树是无向图，所以每条边都会被算两次，最后答案除以 2 即可。

虽然这个表述使用了指数级的限制，但我们知道，最小生成树是有多项式算法的。也可以用椭球法在多项式时间内解最小生成树问题。

装箱问题

设共有 $n$ 个物品， $w_i$ 表示第 $i$ 个物品的重量， $c$ 表示每个箱子的承重， $x_{i, j} \in \{0, 1\}$ 表示是否将第 $i$ 个物品放入第 $j$ 个箱子， $y_i$ 表示是否使用第 $i$ 个箱子。那么装箱问题可以写为 $\begin{matrix} \min\limits_{x, y} & \sum\limits_{i=1}^n y_i \\ \text{s.t.} & \sum\limits_{i=1}^n w_ix_{i, j} \le cy_j & \forall j \in \{1, 2, \dots, n\} \\ & \sum\limits_{j=1}^n x_{i, j} = 1 & \forall i \in \{1, 2, \dots, n\} \\ & x_{i, j} \in \{0, 1\} \\ & y_{i, j} \in \{0, 1\} \end{matrix}$

第一项限制保证了每个箱子装的物品不会超过承重，第二项限制保证了每个物品一定会被装入箱子，且每个物品只装入一个箱子。

匹配问题

设图的点集为 $V$ ，边集为 $E$ 。设 $(i, j) \in E$ 表示从第 $i$ 个点连到第 $j$ 个点的一条有向边， $x_{i, j}$ 表示这条边是否为匹配边。那么一般无向图的最大匹配问题可以写为 $\begin{matrix} \max\limits_x & \sum\limits_{(i, j) \in E} x_{i, j} \\ \text{s.t.} & \sum\limits_{(i, j) \in E} x_{i, j} \le 1 & \forall i \in V \\ & \sum\limits_{(i, j) \in E} x_{i, j} \le 1 & \forall j \in V \\ & x_{i, j} \in \{0, 1\} \end{matrix}$

旅行商问题：
- 满足每个点都有一个入度和一个出度 $\sum_{i}x_{ij}=\sum_{j}x_{ij}=1$
- 增加辅助变量 $u_i$ 保证所有点[0,n]都在0号点的同一个环上，需要满足 $u_{i}-u_{j}+n*x_{ij} \leq n-1, 1 \leq i \neq j \leq n$ ，考虑如果存在一个不包含0号点的环，那么沿着这个环一圈加起来，左侧 $u_{i}$ 全部消掉，不等式不成立，对于全部都在0号点环上的情况，沿着0号点出发依次给 $u_{i}$ 赋值 $1,2,3...$ 即可构造出可行解，因此这个约束与要求是等价的。

幺模矩阵

若一个方阵的行列式值为 $\pm 1$ ，那么称其为幺模矩阵
若矩阵A的任何一个非奇异子方阵都是幺模矩阵，那么称矩阵A是全幺模矩阵，对于整数向量b， $Ax=b$ 的基本可行解都是整数解
全幺模矩阵：
- 若 $A$ $A$ 是全幺模矩阵，则 $A^{T}, [A, I]$ $A^{T}, [A, I]$ 也是全幺模矩阵， $A^{-1}$ $A^{- 1}$ 是整数矩阵
  - 如果取到了含有 $I$ 的列那么按列展开求行列式可得子方阵一定是幺模矩阵
- 判定条件（充分不必要）
  - 如果A的元素为 $0,\pm 1$ ，且每列中非零元素至多有两个使得A的行可以分成两个子集 $I$ 和 $J$ 满足：如果一列中两个非零元素符号相同，则所在行分别属于 $I$ 和 $J$ ，如果符号不同，则所在行同时属于 $I$ 或 $J$ ，则A是全幺模矩阵
  - 如果A的元素为 $0, \pm 1$ ，且每列中至多含有一个非零元素，那么A是全幺模矩阵
- 常见的全幺模矩阵：有向图的关联矩阵

Gomory 割平面法

Gomory 割平面法：在解空间中增添约束去掉分数解空间，不断逼近整数解空间。

考虑一个线性规划问题，假设我们使用单纯形表求解后获得的不是整数解，我们选择一个非整数的变量 $x_i$ ，根据单纯形表有 $x_i + \sum\limits_{j=m+1}^n \bar{a_{i,j}}x_j = \bar{b_i} \qquad \qquad \text{①}$

既然 $x_i$ 不是整数，说明 $\bar{b_i}$ 一定不是整数，当然 $\bar{a_{i,j}}$ 也可能不是整数。

将式 ① 调整一下，变为 $x_i + \sum\limits_{j=m+1}^n \left\lfloor \bar{a_{i,j}} \right\rfloor x_j \le \bar{b_i} \qquad \qquad \text{②}$

显然，式 ① 的解一定是式 ② 的解。

再次调整式 ②，变为 $x_i + \sum\limits_{j=m+1}^n \left\lfloor \bar{a_{i,j}} \right\rfloor x_j \le \left\lfloor\bar{b_i}\right\rfloor \qquad \qquad \text{③}$

容易看出，式 ② 的整数解一定符合式 ③，而原来用单纯形表求出的非整数解就不符合式 ③ 了（因为原来求出的非整数解中，有 $x_i = \bar{b_i} > \left\lfloor \bar{b_i } \right\rfloor$ 以及 $x_j = 0$ ）。我们只要把式 ③ 加入原来的线性规划问题，分数解空间会减小，但是整数解空间不变，对新的限制问题进行求解直至求出整数最优解。

来举个例子，考虑以下线性整数规划问题 $\begin{matrix} \max\limits_x & 3x_1 + 2x_2 \\ \text{s.t.} & 2x_1 + 3x_2 + x_3 = 14 \\ & 2x_1 + x_2 + x_4 = 9 \\ & x \ge 0 \end{matrix}$

用单纯形表解该问题，结果为 $\begin{array}{c|cccc|c} & 0 & 0 & -1/4 & -5/4 & -59/4 \\ \hline x_2 & 0 & 1 & 1/2 & -1/2 & 5/2 \\ x_1 & 1 & 0 & -1/4 & 3/4 & 13/4 \end{array}$

选择 $x_2$ ，加入限制： $x_2 - x_4 \le 2$ ，即 $x_2 - x_4 + x_5 = 2$ 。

用单纯形表求解加入限制后的问题，结果为 $\begin{array}{c|ccccc|c} & 0 & 0 & 0 & -1 & -1/2 & -29/2 \\ \hline x_3 & 0 & 0 & 1 & 1 & -2 & 1 \\ x_1 & 1 & 0 & 0 & 1 & -1/2 & 7/2 \\ x_2 & 0 & 1 & 0 & -1 & 1 & 2 \end{array}$

选择 $x_1$ ，加入限制： $x_1 + x_4 - x_5 \le 3$ ，即 $x_1 + x_4 - x_5 + x_6 = 3$ .

用单纯形表求解加入限制后的问题，结果为 $\begin{array}{c|cccccc|c} & 0 & 0 & 0 & -1 & 0 & -1 & -14 \\ \hline x_3 & 0 & 0 & 1 & 1 & 0 & -4 & 3 \\ x_1 & 1 & 0 & 0 & 1 & 0 & -1 & 4 \\ x_5 & 0 & 0 & 0 & 0 & 1 & -2 & 1 \\ x_2 & 0 & 1 & 0 & -1 & 0 & 2 & 1 \end{array}$

所以原问题的最优解为 $x_1 = 4, x_2 = 1$ ，目标函数值为 $14$ 。

分枝定界法

思想和最优性剪枝或者 min-max 搜索树差不多，在解空间中不断分为两支分别求解，通过上下界进行剪枝优化。

先解原问题，得到整数规划最优解的上界。假设最优解中 $N < x_i < N+1$ 不是整数，就会有两种可能： $x_i \le N$ 或 $x_i \ge N+1$ ，对两种情况分别进行搜索。

如果在某一枝内算出了一个整数解，我们就得到了原整数规划最优解的下界；如果另一枝内线性规划问题的解还没有这个下界来得优，那么那一枝就不考虑了。一个子树的最优解不会比根节点的最优解（可能是分数）更差。

试一试 Gomory 单纯形法的例子。将原问题松弛为线性规划问题后，得到的最优解为 $x_2 = 5/2, x_1 = 13/4$ ，目标函数值为 $59/4$ 。

先探索 $x_2 \le 2$ 的情况，用单纯形表求解得 $\begin{array}{c|ccccc|c} & 0 & 0 & 0 & -1 & -1/2 & -29/2 \\ \hline x_3 & 0 & 0 & 1 & 1 & -2 & 1 \\ x_1 & 1 & 0 & 0 & 1 & -1/2 & 7/2 \\ x_2 & 0 & 1 & 0 & -1 & 1 & 2 \end{array}$

探索 $x_1 \le 3$ 的情况，用单纯形表求解得 $\begin{array}{c|cccccc|c} & 0 & 0 & 0 & 0 & -2 & -3 & -13 \\ \hline x_3 & 0 & 0 & 1 & 0 & 0 & -2 & 2 \\ x_4 & 0 & 0 & 0 & 1 & 0 & -2 & 1 \\ x_2 & 0 & 1 & 0 & 0 & 1 & 0 & 2 \\ x_1 & 1 & 0 & 0 & 0 & 0 & 1 & 3 \end{array}$

得到候选的解 $x_1 = 3, x_2 = 2$ ，目标函数值为 $13$ 。

接下来探索 $x_1 \ge 4$ ，用单纯形表解得 $\begin{array}{c|ccccc|c} & 0 & 0 & 0 & -2 & -1 & -14 \\ \hline x_1 & 1 & 0 & 0 & 0 & -1 & 4 \\ x_3 & 0 & 0 & 1 & -2 & -4 & 3 \\ x_2 & 0 & 1 & 0 & 1 & 2 & 1 \\ x_5 & 0 & 0 & 0 & 0 & 1 & 1 \end{array}$