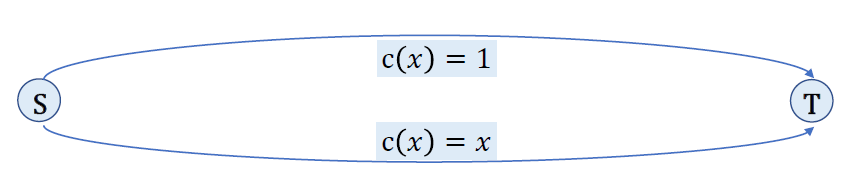斯坦纳树、旅行商问题

本节轮到我们这组做lecture notes，提交上去的是用latex处理的整理结果。这里我把自己的笔记基本更新成和lecture notes一致了，内容更少一些，个别表达有所不同。

斯坦纳树问题

斯坦纳树问题：给定G=(V,E), C:E→R+G=(V,E), \ C:E \rightarrow R^{+}，其中CC满足三角不等式。对于点集S⊆VS \subseteq V，求GG的连通子图G′=(S′,E′), S⊆S′G'=(S', E'), \ S \subseteq S'，使得SS中的点彼此联通，并且选中的边权和最小。显然，最优解的G′G'必定是一棵树，我们记作斯坦纳树，S′∖SS' \setminus S中的点记作斯坦纳点。

斯坦纳树问题的求解是一个NP-Hard问题。在本节中，我们重点关注该问题的近似算法，同时为了简单起见，我们仅讨论完全图上的斯坦纳树。

欧氏平面上的斯坦纳树

欧氏平面上的斯坦纳树：给定平面上的nn个点，用总长尽量短的线段把他们连接起来。注意线段可以在平面上的任意点相交。

欧氏平面上的距离关系自然满足三角不等式。

最优解中，线段在平面上除了给定点外的交点就是斯坦纳点。

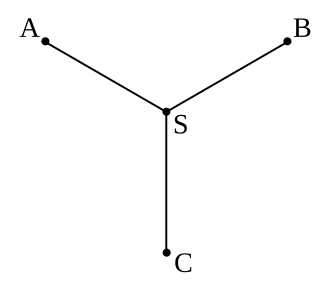
平面斯坦纳树（n = 3） 平面斯坦纳树（n = 4）

从上图看出 n=3n = 3 和 n=4n = 4 的情况，SS、S1S_1 和 S2S_2 是斯坦纳点。n=3n = 3 时，斯坦纳点就是三角形的费马点。

满足三角不等式的斯坦纳树：2-近似算法

容易想到，如果不考虑斯坦纳点，对图GG关于SS的导出子图直接求最小生成树，就是斯坦纳树问题的一个可行解。在满足三角不等式的前提下，我们可以证得这就是一个22-近似的算法，下面给出证明。

算法近似比证明：

记给定点集SS的最小生成树解TT，斯坦纳树问题的最优解T∗T^{*}。可以将T∗T^{*}中的边复制一遍，得到图2T∗2T^{*}。由于图2T∗2T^{*}中的所有点的度数都是偶数且联通，那么一定存在经过SS中所有点的欧拉回路。

从SS中的一点出发，找到任意一条欧拉回路LL。易知LL的长度就是2T∗2T^{*}的边权之和。我们这样构造一个可行解：只走SS中的点，且每个点只走一次，如果遇到了斯坦纳点或者已经走过的点就“跳跃”到下一个点。因为我们是讨论完全图上的斯坦纳树，所以跳跃是允许的，这种跳跃又称为short-cutting。这样依次走完SS中的点，就得到一个可行解T′T'。

举个例子，假定下图是我们对2T∗2T^{*}构造的欧拉回路的一部分，红色代表SS中的点，蓝色则是斯坦纳点。由于aa之后遇到了斯坦纳点，我们要跳跃到bb；在走到cc之后，由于aa已经走过了，我们要直接跳到dd。

01

在满足三角不等式的前提下，直接跳过去不会比沿着欧拉回路LL走过去的距离长，所以有C(T′)≤2C(T∗)C(T') \leq 2 C(T^{*})。又因为T′T'也是一棵SS上的生成树，边权之和不会比最小生成树TT小，因此C(T)≤C(T′)C(T) \leq C(T')。综上所述，有C(T)≤C(T′)≤2C(T∗)C(T) \leq C(T') \leq 2C(T^{*})。近似比上界是2。

然后证明近似比下界也是2：如下图所示，构造这样一个例子，令S={v1,v2,…,vn}S = \{v_1, v_2, \dots, v_n\}。SS中的所有点到中心点的边权值为1，其他边权值都为2。

02_2

对这个例子使用最小生成树求解，得到的树是是不经过中心点的一条链，边权和为2(n−1)2(n-1)。显然，该问题的最优解是利用中心点作为斯坦纳点，边权和为nn，从而得到近似比2n−2n\frac{2n-2}{n}，当n→∞n \rightarrow \infty时，近似比趋近于2。因此近似比的下界为2。

综上所述，最小生成树是满足三角不等式的斯坦纳树问题的22-近似算法。

旅行商问题

背景：

欧拉回路：从s出发，恰好经过每条边最后回到s

欧拉路：恰好经过每条边

哈密尔顿圈：从s出发，恰好经过每个点回到s

哈密尔顿路径：从s出发，恰好经过每个点到达终点t

旅行商问题（TSP）：给定完全图G=(V,E), C:E→R+G=(V,E),\ C:E \rightarrow R^{+}，求边权和最小的哈密尔顿圈。即，确定顶点的一个排列顺序π\pi，使得∑i=1nC(vπi,vπi+1)\sum_{i=1}^{n} C(v_{\pi_{i}}, v_{\pi_{i+1}})最小，其中πn+1=π1\pi_{n+1}=\pi_{1}。

完全图上的旅行商问题也是一个NP-Hard问题。

旅行商问题的近似算法研究

普通完全图上的 TSP 没有很好的近似比。若CC任意，可以证明∀k=2poly(n)\forall k=2^{poly(n)}，都不存在kk近似算法。其中poly(n)poly(n)是nn的多项式。

证明：考虑哈密尔顿圈问题，已知判断图G1=(V,E1)G_{1}=(V,E_{1})是否含哈密尔顿圈是一个NPC问题。构造完全图G=(V,E)G=(V,E)，对G求TSP问题。其中，EE中一条边ee的边权定义如下：

C(e)={1e∈E1nke∉E1C(e) = \begin{cases} 1 & e \in E_{1} \\ nk & e \not\in E_{1} \end{cases}

反证法：假设存在TSP的kk-近似算法，利用算法对GG求TSP近似解。那么若TSP的最优解Copt=nC_{opt} = n，即G1G_{1}中存在哈密尔顿圈，TSP近似解满足CA≤nkC_{A} \leq nk；否则最优解一定满足Copt≥nk+n−1C_{opt} \geq nk + n-1，即G1G_{1}中不存在哈密尔顿圈，TSP近似解CA≥nk+1C_{A} \geq nk + 1。

这样一来，由这种近似算法求解后，根据近似解与nknk的大小关系，就可以反推G1G_{1}的哈密尔顿圈问题。但是，哈密尔顿圈是一个NP问题，不能被归约到多项式时间求解，也就证明了不存在旅行商问题的kk-近似算法。考虑到问题的编码长度与多项式规约，保证k=2poly(n)k=2^{poly(n)}，完全图的输入规模仍然是 nn 的多项式。

推广：同理可以证明装箱问题的近似比不会小于等于32\frac{3}{2}，因为判断2个箱子能否装下物品是NP问题，如果存在近似比小于32\frac{3}{2}的近似算法，直接用它求解装箱问题，有：如果近似解用了3个箱子，说明最优解2个箱子可以装下；如果近似解用了多于3个箱子，就说明最优解2个箱子装不下。这样一来就解决了判断2个箱子能否装下物品这个NP问题，因此，不存在近似比小于等于32\frac{3}{2}的装箱问题近似算法。

满足三角不等式的TSP问题

根据前面的证明，我们知道普通完全图上的旅行商问题难以得到较好的近似算法。因此，我们再给该问题加上一定的限制：在距离函数CC满足三角不等式的前提下，旅行商问题就有较好的近似算法。接下来讨论此前提下的旅行商问题。

最小生成树松弛算法

记旅行商问题最优解为H∗H^{*}。求图GG的最小生成树T∗T^{*}，显然C(T∗)≤C(H∗)C(T^{*}) \leq C(H^{*})。最小生成树松弛算法过程如下：

把T∗T^{*}中的边复制一遍得到图GeG_{e}。GeG_{e}的所有点度数都为偶数且相互连通，因此一定存在欧拉回路。与斯坦纳树问题同理，任选一条欧拉回路应用short-cutting（此处要保留最后一个点），得到点的排列π\pi为TSP的可行解，并生成哈密尔顿圈HcH_{c}。由三角不等式，易知C(Hc)≤C(Ge)=2C(T∗)C(H_{c}) \leq C(G_{e}) = 2 C(T^{*})。

综上所述，C(Hc)≤C(Ge)=2C(T∗)≤2C(H∗)C(H_{c}) \leq C(G_{e}) = 2 C(T^{*}) \leq 2C(H^{*})，因此该算法近似比上界为2。

构造例子如下图所示：

04

完全图GG共有2n+12n+1个顶点，中心点v0v_{0}到外围每个点的距离是11，外围相邻的两个点距离也是11，其他边权都为2（未在图中标出）。容易求得最小生成树T∗T^*为v0v_{0}为中心的星图。如果对GeG_{e}选择欧拉回路v0v1v0v3v0…v2n−1v0v2v0v4…v2nv0v_0v_1v_0v_3v_0 \dots v_{2n-1}v_0v_2v_0v_4 \dots v_{2n}v_0，再去重复点做short-cutting得到HcH_c：v0v1v3…v2n−1v2…v2nv0v_0v_1v_3 \dots v_{2n-1}v_2 \dots v_{2n}v_0，则有C(Hc)=2(2n−1)+2=4nC(H_c) = 2(2n-1)+2 = 4n。易知最优解的C(H∗)=2n+1C(H^{*})=2n+1，从而确定该算法近似比下界为2。

因此，该算法的近似比是2。

MST松弛改进

考虑MST松弛算法的改进空间，所有边复制一遍的操作可能与最优解之间间隙比较大，我们尝试只给生成树中的奇度数点添边。显然生成树中的奇度数点会有偶数个，存在完美匹配，即求一个T∗T^{*}中奇度数点之间的最小权完美匹配M∗M^{*}，得到Ge=T∗∪M∗G_{e}=T^{*}\cup M^{*}（这里的并是边集的相加，即如果两个集合中都有这条边，那么在并中会有两条一样的边）。在GeG_{e}上取任意的欧拉回路，生成一个近似解HcH_{c}，有C(Hc)≤C(T∗)+C(M∗)C(H_{c}) \leq C(T^{*}) + C(M^{*})。接下来证明该算法的近似比为32\frac{3}{2}。

分析最优解H∗H^{*}，H∗H^*是一个环。考虑取出其中的生成树中的奇度数点依次连起来，不妨设为2n2n个奇度数点t1,t2,…t2nt_1,t_2,\dots t_{2n}，他们之间连有2n2n条边。显然，按照次序，(t1−t2,…t2n−1−t2n)(t_1 -t_2,\dots t_{2n-1} - t_{2n})和(t2−t3,…t2n−t1)(t_2 - t_3, \dots t_{2n} - t_{1})就是两组完美匹配M1,M2M_1,M_2，满足C(H∗)≥C(M1)+C(M2)≥2C(M∗)C(H^{*}) \geq C(M_1)+C(M_2) \geq 2C(M^{*})，所以C(M∗)≤12C(H∗)C(M^{*}) \leq \frac{1}{2}C(H^{*})。

综上所述，有C(Hc)≤C(T∗)+C(M∗)≤32C(H∗)C(H_{c}) \leq C(T^{*}) + C(M^{*}) \leq \frac{3}{2}C(H^{*})，改进后近似比的上界为32\frac{3}{2}。

构造例子如下图所示，证明其下界也为32\frac{3}{2}：

05

完全图上面一行有nn个顶点，下面一行有n+1n+1个顶点。图中画出的边权值为1，其他顶点间的距离由所给边下的最短路长确定。易知C(Hc∗)=2n+1C(H^{*}_{c}) = 2n+1，环绕一圈即为最优解。若最小生成树T∗T^*为v1v2…v2n+1v_1v_2 \dots v_{2n+1}，有C(T∗)=2nC(T^*)= 2n，则有奇度数点的最小完美匹配M∗M^*为v1v2n+1v_1v_{2n+1}，C(M∗)=nC(M^*)=n。综上得到近似比2n+n2n+1\frac{2n+n}{2n+1}，当n→∞n \rightarrow \infty时，近似比趋近于32\frac{3}{2}，得证。

哈密尔顿路径问题

哈密尔顿路径问题指在赋权完全图上求边权和最小的哈密尔顿路，这里我们同样考虑满足三角不等式的情况。类似于旅行商问题，也可以得到类似的MST松弛算法：求GG的最小生成树T∗T^{*}，做奇度数点中除去任意两点的最小权完美匹配M∗M^{*}，得到Ge=T∗∪M∗G_{e}=T^{*} \cup M^{*}再做short-cutting。其中，去掉的这两点在GeG_{e}中度数仍为奇数，作为哈密尔顿路径的起点和终点。

类似地，把最优解中除去起点、终点外的T∗T^{*}奇度数点摘出来，可以得到两组匹配，且剩余一条边（因为完美匹配是去掉了两个奇度数点的），因此仍然可以证明算法近似比为32\frac{3}{2}。另外，要解决去掉任意两点的最小权完美匹配的求解问题，这里可以引入两个虚拟节点a,ba,b，连接到所有奇度数点并设置边权为0，则在最小权完美匹配中a，b一定会各自匹配到一个奇度数点，就相当于去掉了任意两个点后的完美匹配最优解。

06

固定起点的哈密尔顿路径问题

如果指定了起点SS求边权和最小的哈密尔顿路，意味着SS的度数有可能是偶数，那么就要尝试在图GeG_{e}中调整起点SS的度数为奇数，我们通过给SS加一条边来解决。在T∗T^*中引入误点的概念，误点包括：

  • V∖{S}V \setminus \{ S \}中的奇度数点

  • SS，若SS是偶度数点

误点的度数是需要加边调整的。这样一来，如果SS的度数是偶数，我们就会尝试加边改为奇度数点。可以证明误点一定是奇数个：如果SS为奇度数点，那么奇度数点共有偶数个，去掉SS为奇数个；如果SS为偶度数点，那么奇度数点共有偶数个，算上SS仍为奇数个。

对所有误点求去掉任一点的最小权完美匹配M∗M^{*}（类似于前面去掉任意两点求解的算法，不多阐述），做Ge=T∗∪M∗G_{e}=T^{*}\cup M^{*}，再做short-cutting就可以得到一个解HcH_{c}。

对于图GeG_{e}，考虑起点SS的两种情况：

若SS为奇度数点，则SS不是误点，SS和求完美匹配时去掉的点直接分别构成起点和终点；

若SS为偶度数点，并且没有被匹配的误点是SS，那么图GeG_{e}中全部都是偶度数点，任意选取一个与SS相连的点AA，删去他们之间的边，这样图中一定存在着从SS为起点AA为终点的欧拉路径，即可构成哈密尔顿路。

可以证明，对于固定起点的哈密尔顿路径求解，以上算法的近似比仍然是32\frac{3}{2}：

分析最优解H∗H^{*}，考虑取出其中的误点依次连起来，不妨设为2n+12n+1个误点t1,t2,…t2n+1t_1,t_2,\dots t_{2n+1}，他们之间连有2n2n条边。显然，按照次序，(t1−t2,…t2n−1−t2n)(t_1 -t_2,\dots t_{2n-1} - t_{2n})和(t2−t3,…t2n−t2n+1)(t_2 - t_3, \dots t_{2n} - t_{2n+1})就是两组完美匹配M1,M2M_1,M_2，因此仍然满足C(H∗)≥C(M1)+C(M2)≥2C(M∗)C(H^{*}) \geq C(M_1)+C(M_2) \geq 2C(M^{*})，也就可以证明MST松弛算法的近似比为32\frac{3}{2}。

固定起点、终点的哈密尔顿路径问题

对于固定起点和终点的哈密尔顿路径问题，算法近似比不再是32\frac{3}{2}。首先介绍算法过程，仍然是MST松弛算法，同样引入误点的概念：

  • V∖{S,T}V \setminus \{ S,T \}中的奇度数点

  • {S,T}\{ S,T \}中的偶度数点

容易知道误点一定有偶数个，在误点中做最小权完美匹配得到M∗M^{*}。那么在图Ge=T∗∪M∗G_{e}=T^{*} \cup M^{*}中，S,TS,T的度数为奇数，其他点的度数为偶数，所有点都是联通的，因此存在从SS出发到TT的欧拉路径，任选构造一条从SS到TT的欧拉路径就得到了一个点的排列π\pi。

注意，在π\pi中TT可能在中间就出现过了，为了保证TT是终点，在做short-cutting得到哈密尔顿路径HcH_{c}的过程中，把中间出现的TT跳跃掉即可，只保留终点的TT。这样就可以得到一个SS为起点，TT为终点的哈密尔顿路径近似解了。

对于固定起点、终点的哈密尔顿路径求解，算法近似比不再是32\frac{3}{2}。下面这个例子可以说明，近似比至少是53\frac{5}{3}：

07

完全图上有如图所示88个点，部分边权已经在图上标出，其余边权设置为该图上的最短路径长度。容易知道最优解C(H∗)=3N+6C(H^{*})=3N+6，但按照以上算法，哈密尔顿路径可以取到C(Hc)=5N+6C(H_{c})=5N+6。因此得到近似比下界53\frac{5}{3}。

下面证明算法近似比上界就是53\frac{5}{3}：

同样分析最优解和匹配之间的关系，考虑不等式C(T∗)+C(H∗)≥3C(M∗)C(T^{*})+C(H^{*}) \geq 3C(M^{*})是否成立，如果成立的话，由于C(T∗)C(T^{*})是C(H∗)C(H^{*})的下界，就可以得到C(M∗)≤23C(H∗)C(M^{*}) \leq \frac{2}{3}C(H^{*})。

考虑图Ge=T∗∪H∗G_{e}=T^{*} \cup H^{*}，由于H∗H^{*}是一条哈密尔顿路径，因此只有起点和终点的度数奇偶性发生改变，图GeG_{e}中仍然有偶数个误点，T∗T^{*}中除了S,TS,T以外的奇度数点仍然为奇度数点。容易推出，T∗T^{*}中的奇度数点在GeG_{e}中都属于误点（包括S,TS,T）。

由于最优解H∗H^{*}中包含一组误点的匹配，即从H∗H^{*}中选出所有GeG_{e}中的误点，按序两两选出误点之间的匹配边，称这个匹配为EE，有C(E)≥C(M∗)C(E) \geq C(M^{*})。考虑图Q=Ge∖EQ=G_{e} \setminus E，得到的图所有点的度数都是偶数，由于E⊆H∗E \subseteq H^{*}，因此T∗⊆QT^{*} \subseteq Q，QQ是联通的。综上可以得到QQ是欧拉图，一定存在一条欧拉回路，这条回路包含了两组误点的完美匹配，满足C(Q)≥2C(M∗)C(Q) \geq 2C(M^{*})，所以C(T∗)+C(H∗)≥3C(M∗)C(T^{*})+C(H^{*})\geq 3C(M^{*})，也就证明了近似算法的近似比上界53\frac{5}{3}。

所以对于固定起点和终点的哈密尔顿路径问题，以上算法近似比是53\frac{5}{3}。