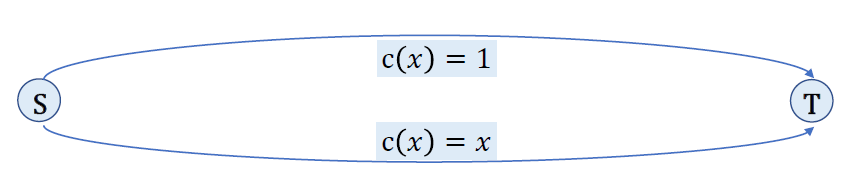AOR6 装箱问题

装箱问题

First-Fit算法

引入

渐进比： 算法A如果对于任意的实例 $I$ ，存在一个常数$k$，满足$A(I) \leq \alpha OPT(I) + k$，称 $\alpha$ 的下确界为A的渐近比。与近似比相比，渐进比后面多了一个常数$k$。

一维装箱问题： 给定 $n$ 个物品，体积在$(0,1]$之间，求最少需要多少个体积为 $1$ 的箱子可以装下。

• 两个箱子能否装下所有物品是NPC问题；装箱问题不存在近似比小于$\frac{3}{2}$的多项式近似算法（unless P=NP）。这两条可以推嘛？
• 传统的装箱算法有Next Fit，First Fit，Best Fit，Harmonic Fit等，尽管近似比没有什么乐观的结果，我们本节可以关注一下它们的渐进比。

Next Fit (NL)

Next Fit：如果现在这个箱子能装下，就把物品放进去；否则关闭它，并打开一个新的箱子来放物品。

• 线性时间算法，$NL(I) \leq 2 OPT(I) - 1$。证明：任意两个相邻箱子物品体积之和一定大于1。考虑$NL(I)=2m$或者$NL(I)=2m+1$，都有$OPT(I) \ge m+1$。

Any Fit

不关闭箱子。如果有多个箱子可以放，可以采用不同的策略：

• First Fit(FF)：选择第一个能装的箱子
• Best Fit(BF)：选择剩余体积最小的箱子
• Worst Fit(WF)：选择剩余体积最大的箱子
• Almost Worst Fit(AWF)：选择剩余体积第二大的箱子

其中WF可以跟NF一样差，其他的都可以做到1.7的渐进比。

First Fit渐进比分析

结论： 对于任意实例有$FF(I) \leq 1.7OPT(I) + \frac{4}{5}$

• 最新进展可以去掉$\frac{4}{5}$，但权函数要依赖于解的情况
• First Fit算法在正态分布下的渐近比为1，可以满足大规模应用的求解

分析： 对于 $I = \{ a_1, \dots, a_n\}, a_i \in (0, 1]$，证明对任意 $I, \ FF(I) \leq 1.7OPT(I) + \frac{4}{5}$。

• 思路：构造一个均摊权重函数$w$，有 $a_i \rightarrow w(a_i)$。定义$w(I) = \sum_{i=1}^{n}w(a_{i}) = \sum_{j=1}^{FF(I)}w(B_{j}) = \sum_{j=1}^{OPT(I)}w(B_{j}^*)$，将$w(I)$作为中间变量。这里的 $B$ 指箱子，$w(B)$ 是针对箱子内的物品计算权重。

• 如果能满足 $w(I) \leq 1.7 OPT(I) \\ FF(I) \leq w(I) + \frac{4}{5}$，可以证明出结论。对于第一条，我们希望对任意的 $B_j^*$，有 $w(B^*_j) \le 1.7$；对于第二条，我们希望对任意的 $B_j$，在平均意义上 差不多$w(B_j) \ge 1$。

证明：

• 定义一个特殊的权重函数$w(a)=\frac{6}{5}a+v(a)$，其中$v$称为bonus函数，定义为

  $v(a)=\left\{ \begin{aligned} a = 0 & & a\leq \frac{1}{6} \\ a = \frac{3}{5}(a - \frac{1}{6}) & & \frac{1}{6} \leq a \leq \frac{1}{3} \\ a = \frac{1}{10} & & \frac{1}{3} \leq a \leq \frac{1}{2} \\ a = \frac{4}{10} & & a > \frac{1}{2} \end{aligned} \right.$。可以看到根据$a$的大小分成4类，不妨称为tiny, small, medium, big。

  函数图像如下所示：

  

• 首先考虑第一条：我们希望对任意的 $B_j^*$，有 $w(B^*_j) \le 1.7$

  • 如果$B_j^*$没有big item的话，$\frac{6}{5}a$这部分最坏情况（完全装满）为1.2，bonus函数部分最坏情况是有三个体积为$\frac{1}{3}$的item，为0.3，所以此时有$w(B^*_j) \le 1.5 \le 1.7$
  • 如果$B_j^*$有big item的话，$\frac{6}{5}a$这部分最坏情况（完全装满）为1.2，big item能带来0.4的bonus，剩下的体积不足 $\frac{1}{2}$，最多带来0.1的bonus。所以此时有$w(B^*_j) \le 1.2+0.4+0.1 = 1.7$

• 然后考虑第二条：$FF(I) \leq w(I) + \frac{4}{5}$，我们希望对任意的 $B_j$，补上0.8，就能在平均意义上让$w(B_j) \ge 1$。

  • 考虑什么情况下一定有$w(B_j) \ge 1$：
    • 如果$B_j$里的物品总体积大于等于$\frac{5}{6}$，$w(B_j) \ge 1.2 * 5 / 6 = 1$
    • 如果$B_j$里有一个big item，$w(B_j) \ge 1.2 * 0.5 + 0.4 = 1$
    • 如果 $B_j$里有两个medium item，$w(B_j) \ge 1.2 * \frac{2}{3} + 0.2 = 1$
  • 所以如果一个箱子满足$w(B_j) < 1$，一定满足
    • 它没有big item
    • 它最多只能有一个medium item
    • 它装的物品总体积小于$\frac{5}{6}$
  • 假设在$FF$装法下，有 $k$ 个箱子是$w(B_j) < 1$的。证明给这部分补0.8，平均权值能大于等于1。
    • 如果 $k=1$，这个箱子加上前一个箱子的体积一定大于1，那么两个箱子合起来的权值大于1.2，加上补的0.8再平均，就能让平均的权值大于等于1。
    • 如果 $k \ge 2$：

      • 箱子里只有1个item的话，已知它不能是big item，所以总体积小于等于 $1/2$。那么这样的箱子最多一个，而且肯定是最后一个$w(B_j) < 1$的箱子，称为$B_p$。

      • 箱子里至少有两个item的话，最多一个箱子是总体积小于$2/3$的，并且它只能是倒数第二个$w(B_j) < 1$的箱子（如果$B_p$存在）或者最后一个这样的箱子（如果$B_p$不存在）。称它为$B_q$。

      • 也就是说$w(B_j) < 1$的箱子从前往后是这样一个序列，前面都是总体积大于等于$2/3$的，然后$B_q$，$B_p$。

      • 引理：如果两个权值小于1的箱子B和C满足：B在C前面，$\frac{2}{3} \le c(B) < \frac{5}{6}$，C有至少两个物品，则$h = \frac{6}{5}c(B) + v(C) \ge 1$。

        • 证明：如图所示，假定$c(B) = \frac{5}{6} - z, z \in (0, \frac{1}{6}]$。则有$x > 1 - (\frac{5}{6} - z) = \frac{1}{6} + z \in (\frac{1}{6}, \frac{1}{3}], y \in (\frac{1}{6}, \frac{1}{3}]$。

          所以 $v(x) > \frac{3}{5}(\frac{1}{6} + z - \frac{1}{6}) = \frac{3}{5}z,\ v(y) > \frac{3}{5}z$

          所以 $h = \frac{6}{5}c(B) + v(C) = \frac{6}{5}(\frac{5}{6} - z) + v(x) + v(y) \ge 1$

          

      • 所以，对 $i = 1, 2, \dots, k-2$，有 $\frac{6}{5}c(B_i) + v(B_{i+1}) \ge 1$。这部分有k-2的权值。

      • 对最后两个箱子，有 $c(B_{k-1})+c(B_k) > 1$。这部分有1.2的权值。

      • 以上两部分再加上补的0.8，我们就拿到了k的权值，平均意义上就大于等于1了。

• 由这两条，我们就证明了$FF(I) \leq 1.7OPT(I) + \frac{4}{5}$。

First Fit Decreasing(FFD)

FFD：按照从大到小的顺序排列item之后再使用FF算法。是一个offline的算法。有两个结论：

• 近似比：$FFD(I) \leq \frac{3}{2}OPT(I)$
  • 卡满例子：$[\frac{1}{2},\frac{1}{4},\frac{1}{4}],[\frac{1}{3},\frac{1}{3},\frac{1}{3}]$
• 渐进比：$FFD(I) \leq \frac{11}{9}OPT(I) + \frac{6}{9}$。证明很复杂。
  • 卡满例子：$\{ 6 \times (\frac{1}{2}+\epsilon), 6 \times (\frac{1}{4}+2\epsilon), 6 \times (\frac{1}{4}+\epsilon), 12 \times (\frac{1}{4}-2\epsilon) \}$
• 本文开头提到的NPC问题：判定一堆物品是否可以塞在两个箱子里。FFD 是该问题最优的绝对近似比算法（即不存在任何一个近似算法的绝对近似比$<\frac{2}{3}$）。

Karmarkar and Karp算法

如果我们允许渐进比的式子尾项不是常数，装箱问题能得到一些更好的结果：

• $A(I) \le \mathrm{OPT(I)} + O(\log^2 {\mathrm{OPT}})$
• $A(I) \le \mathrm{OPT(I)} + O(\log {\mathrm{OPT}} * \log\log \mathrm{OPT})$
• $A(I) \le \mathrm{OPT(I)} + O(\log {\mathrm{OPT}})$ （2017，最新进展）

我们接下来要介绍的就是第一种，称为Karmarkar and Karp算法。

引入：Configuration LP

问题描述

对于$I = \{ a_1, \dots, a_n\}$，假设item共有 $m$ 种不同的体积，记为 $s_1, s_2, \dots, s_m$，每种体积$s_i$有物品$b_i$个。

对于一个箱子，我们可以计体积为 $s_1$ 的物品放几个，$s_2$ 的放几个，…，$s_m$ 的放几个。这样得到的一个箱子的装箱方案称为configration。

假设一共有$N$个不同的方案，记 $t_{ij}$ 表示第 $j$ 个方案中，体积为 $s_i$ 的物品放了几个。

记$x_{j}$表示使用了第 $j$ 种方案的箱子用了几个。

那么，我们能写出 bin packing 的线性规划问题：$\begin{matrix} \min\limits_x & \sum\limits_{j=1}^N x_j \\ \text{s.t.} & \sum\limits_{j=1}^N t_{ij}x_j \ge b_i & \forall i \in \{1, 2, \dots, m\} \\ & x_j \ge 0 & \forall j \in \{1, 2, \dots, N\}\end{matrix}$

理解一下：求最小的箱子数量，要满足：对于每种物品体积，我们提供的装箱方案为它预留的空间都是足够的。这个线性规划称为Configuration LP。

基本思路

定理：configration LP可以在$m$和$\log(n/s_{m})$的多项式时间内得到误差不超过1的解。其中，这里的$s_{m}$表示物品的最小体积。

• 大概解法：对$x_{i}$做线性规划，近似的可行解
• 定义$SIZE(I) = \Sigma s_i$，如果$s_{m}\leq 1/SIZE(I)$，那么先去掉所有$\leq 1/SIZE(I)$的物品，最后把他们通过FF或者NF算法加回来，相比于最优解是不会产生误差的（后面证明）。因此可以认为$s_{m} > 1/SIZE(I)$，所以这个线性规划可以在多项式时间内解决。
• 但是得到的是一个分数解，也就是说configuration可能是被切开的，那么我们需要对解做一个rounding。如果直接向上取整的话，只能得到一个$OPT(I)+m$的解。所以这里向下取整，得到一个整数解和剩余的分数解，递归对分数解做线性规划。
  • 得到整数解，已经pack的item set就是$I_z$，有$SIZE(I-I_z)\le m$，继续这样做下去。
  • 这里可以保证划分为两个字问题后得到的仍然是全局最优解，首先划分后两个问题解的和一定不会比全局解更优，又由于分为两个子问题求，每个子问题的局部最优解不会比全局最优解的对应子部分更差，子问题局部最优解之和一定也不会比全局更差，因此二者相等。

###近似算法

具体介绍这个渐进比为 1 的近似算法。记 $N(I)$ 表示该算法对 bin packing 的实例 $I$ 算出来的答案，我们将要证明 $N(I) \le \text{OPT}_{LP}(I) + O(\log^2\text{OPT}_{LP}(I))$。算法步骤如下：

• 记 $SIZE(I)$ 表示实例 $I$ 中物品的体积总和，先将体积小于 $\frac{1}{SIZE(I)}$ 的物品拿走。等其它物品用迭代算法分配完后，再把小的物品用 first fit 安排进去。

• 使用迭代算法分配剩下的物品。

最后分配小物品

为什么最后分配“小”的物品不影响结论呢？下面先证明一个引理。

引理：设 $I$ 为 bin packing 问题的实例，$g$ 是一个 0~1 之间的实数。我们称体积至少为 $\frac{g}{2}$ 的物品为“大”物品，其它物品是“小”物品。我们首先分配大物品，设一共用了 $A$ 个 bin。此时再用 first fit 把小物品也分配进去，则总共使用的 bin 数至多为 $\max(A, (1+g)c(I)+1)$。

证明：设总共使用的 bin 数量为 $B$。如果最后的 first fit 没有再开新的 bin，那么 $B = A$；否则至多有一个 bin 体积小于 $1 - \frac{g}{2}$，那么我们可以推出 $c(I) \ge (1 - \frac{g}{2})(B-1)$，再结合 $0 \le g \le 1$，就有 $B \le \frac{2}{2-g}c(I) + 1 \le (1+g)c(I)+1$。

回到我们的算法，算法的第 1 步其实就是让 $\frac{1}{SIZE(I)} = \frac{g}{2}$，即 $SIZE(I) = \frac{2}{g}$。只要有 $c(I) \ge 2$（$SIZE(I) < 2$ 用 first fit 就行了，反正要证的是渐进比），那么用 first fit 分配小物品后，使用的总 bin 数就是 $(1 + \frac{2}{SIZE(I)})SIZE(I) + 1 = SIZE(I) + 3$（然后和 $A$ 取个 max），不改变我们渐进比为 1 的结论。下面我们只要证明 $A$ 也符合结论就行了。

迭代算法

下面说明要用到的迭代算法，并证明算法的结果仍然符合渐进比为 1 的结论。每一次迭代考虑当前的实例 $I$，进行以下步骤：

step 1 求LP

求出 configuration LP 的解。设第 $j$ 个 configration 用了 $x_j$ 次，由于 LP 只有 $m$ 个限制，那么非零量至多只有 $m$ 个（所以不用担心因为非零量太多直接变成指数级算法）。

step 2 rounding

把实例 $I$ 拆成两部分，$I_1$ 包含了解的整数部分（即 $\left\lfloor x \right\rfloor$），$I_2$ 包含了解的小数部分（即 $x - \left\lfloor x \right\rfloor$）。由于我们使用的 configration 种数至多为 $m$，那么小数部分物品的体积总和不超过 $m$。

容易发现，$I_1$ 的最优解就是恰好放满 $\text{OPT}_{LP}(I_1)$ 个 bin，那么容易有 $\text{OPT}_{LP}(I_1) + \text{OPT}_{LP}(I_2) = \text{OPT}_{LP}(I)$。

举个例子：

假如有 2 种物品 $s_1, s_2$ 和 2 种 configration。

第 1 个configration有 3 个 $s_1$ 与 1 个 $s_2$；

第 2 个configration有 1 个 $s_1$ 与 3 个 $s_2$。

Configuration LP 的解为 2.5 个 configration 1 与 1.5 个 configration 2。

那么我们把 $I$ 拆成两个部分，

$I_1$ 里有 $3 \times 2 + 1 \times 1 = 7$ 个 $s_1$ 和 $1 \times 2 + 3 \times 1 = 5$ 个 $s_2$，

$I_2$ 里有 $3 \times 0.5 + 1 \times 0.5 = 2$ 个 $s_1$ 和 $1 \times 0.5 + 3 \times 0.5 = 2$ 个 $s_2$。

step 3 harmonic grouping

把 $I_2$ 中的所有物品按体积总大到小排序，设为 $s_1 \ge s_2 \ge \dots$。

我们把这些物品分堆：首先找到最小的 $n_1$，把 $s_1$ 到 $s_{n_1}$ 分成第一堆，且堆内物品体积总和至少为 2；再找到最小的 $n_2$，把 $s_{n_1+1}$ 到 $s_{n_2}$ 分成第二堆，且堆内体积总和至少为 2；…这样分成 $r$ 堆，显然r只有最后一堆的体积总和可能小于 2。

由于每个物品的体积都至多为 1，每一堆的体积总和肯定小于 3。还容易发现，由于物品是按体积从大到小排序的，有 $n_1 \le n_2 \le \dots \le n_{r-1}$。

接下来，我们去掉第一堆和第 $r$ 堆。在第 2 到 $r-1$ 堆中，对于第 $i$ 堆，我们只留下最大的 $n_{i-1}$ 个物品（去掉剩下的 $n_i - n_{i-1}$ 个物品），并且把这些物品的体积都放大到第 $i$ 堆里最大的体积。将我们留下来的物品构成实例 $I'$。

不难注意到，如果我们把 $I'$ 也进行分堆，那么 $I'$ 里第一堆的物品数和 $I_2$ 里第一堆的物品数相同，但体积都没有 $I_2$ 第一堆的大，其它堆也是如此。所以我们有 $\text{OPT}(I') \le \text{OPT}(I_2)$。我们只要把 $I'$ 作为新一轮迭代的实例进行迭代即可。

不过，我们要迭代多少轮呢？注意到 $I_2$ 分堆后，每一堆的体积至少为 2，那么 $I'$ 中体积不同的物品种数至多为 $\frac{SIZE(I_2)}{2}$。别忘了我们在第二步中发现的结论：小数部分物品的体积总和不超过体积不同的物品种数。所以每一轮 $I_2$ 的体积都会折半，那么 $\log c(I)$ 轮之后迭代就会结束。

最后我们再来看看被我们去掉的物品总体积是多少。

首先，我们去掉了第一堆和第 $r$ 堆，这两堆的体积之和至多为 6。

再来看第 2 堆到第 $r-1$ 堆。对于第 $i$ 堆，我们去掉了 $n_i - n_{i-1}$ 个物品，它们的体积均值不会超过 $\frac{3}{n_i}$（只考虑小的值，均值会变小）。我们来求个和

$\begin{matrix} & 6 + \sum\limits_{i=2}^{r-1}(n_i-n_{i-1})\frac{3}{n_i} \\ = & 6 + 3\sum\limits_{i=2}^{r-1}(\frac{1}{n_i} + \frac{1}{n_i} + \dots + \frac{1}{n_i}) \\ \le & 6 + 3\sum\limits_{i=2}^{r-1}(\frac{1}{n_{i-1}+1} + \frac{1}{n_{i-1}+2} + \dots + \frac{1}{n_i}) \\ \le & 6 + 3\sum\limits_{i=1}^{n_{r-1}} \frac{1}{i} \end{matrix}$

别忘了我们一开始就把体积小于 $\frac{1}{SIZE(I)}$ 的物品拿走了，那么 $n_{r-1} \le 3 \div \frac{1}{SIZE(I)} = 3c(I)$，那么去掉的物品总体积就是 $O(\log SIZE(I))$ 的了。

我们最后再把这些去掉的物品 first fit 一下就好了。我们知道 first fit 近似比是 1.7 的，不会改变大 O 的结论。

回顾一下

每次迭代都会把当前实例 $I$ 分成 $I_1$ 和 $I_2$。$I_1$ 里的物品由于恰好装满箱子，肯定是最优解的一部分，那么比最优解差的部分就来自于 $I_2$ 中被去掉的物品。而 $I_2$ 中被去掉的物品总体积为 $O(\log SIZE(I))$，迭代最多进行 $\log SIZE(I)$ 次，所以算法的结果就是 $\text{OPT}_{LP}(I) + O(\log^2 SIZE(I)) \le \text{OPT}_{LP}(I) + O(\log^2\text{OPT}_{LP}(I))$，这就完成了证明。