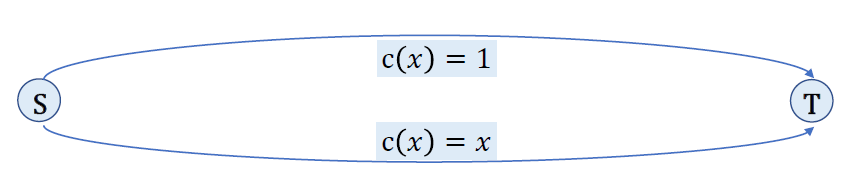AOR4 贪心算法、独立系统、拟阵

贪心算法、独立系统、拟阵

基本概念

独立系统与独立集

• 独立系统： 对于集合系统 $(E, \mathscr{F})$ ，其中 $E$ 是有限基本元素集合，$\mathscr{F} \in 2^E$，若满足：

  • (M1) $\empty \in \mathscr{F}$
  • (M2) 若 $Y \subseteq X \in \mathscr{F}$，则 $Y \in \mathscr{F}$。（包含的封闭性）

  则 $(E, \mathscr{F})$ 是一个独立系统。

• 独立集：$\mathscr{F}$ 中的元素称为独立集。

$\mathscr{F}$ 可以看作某种规则，$\mathscr{F}$ 中的元素就是满足规则的集合。比如定义规则 $\mathscr{F} = \{T\subseteq E, |T| \le K\}$，$(E, \mathscr{F})$ 就是一个符合定义的独立系统，独立集就是模不大于 $K$ 的子集。

基、相关集与圈

• 基： 对于 $F \subseteq E$，若 $T \subseteq F$ 是 $F$ 上的独立集，且 $\forall\ e \in F,\ e \notin T$，都有 $T \cup e$ 就不是独立集，则 $T$ 是 $F$ 上的极大独立集，又称 $T$ 是 $F$ 的一个基。
• 相关集：$2^E\backslash\mathscr{F}$ 中的元素称为相关集。
• 圈： 对于相关集 $T$，若 $T$ 去掉任意一个元素都变成独立集，则 $T$ 是极小相关集，又称 $T$ 是一个圈。

在上面的例子中，基就是模等于 $K$ 的子集，相关集就是模大于 $K$ 的子集，圈就是模等于 $K+1$ 的子集。

秩、下秩与秩商

对于 $E$ 的子集 $F\subseteq E$，有：

• 秩（上秩）：$\gamma(F) = \max\{\ |Y|: Y\subseteq F,\ Y\in \mathscr{F}\ \}$。即模最大的独立集的元素个数。
• 下秩：$\rho(F) = \min\{\ |Y|: Y$ 是 $F$ 的基 $\}$。即模最小的极大独立集的元素个数。
• 秩商：$\displaystyle\mathscr{q}(E,\mathscr{F}) = \min_{F\subseteq E} \frac{\rho(F)}{\gamma(F)}$。即找到集合 $E$ 的一个子集 $F$, 使得下秩和上秩的比值最小（感性理解就是下秩上秩差别最大），秩商表示这个比值。

容易想到，模最大的独立集也是极大独立集，所以其实上秩下秩分别是模最大和最小的基的元素个数；秩商小于等于1。

优化问题

我们前面提到过的很多组合优化问题都可以归结为独立集系统的问题。

记问题为 $(E,\mathscr{F},C)$ ，其中 $C:E\rightarrow R^+$ 表示每个元素的权重。对 $F \in E$，记 $C(F)$ 为 $F$ 的权重，一般而言， $C(F) = \Sigma_{e \in F} C(e)$。我们有两种基本优化问题：

• 极大化问题 $(E,\mathscr{F},C)$ ：寻找权重最大的独立集（结果也是极大独立集）
• 极小化问题 $(E,\mathscr{F},C)$ ：寻找权重最小的极大独立集

组合优化问题的例子

最小生成树问题：

对于连通无向图 $G=(V,E)$，边权 $C:E\rightarrow R^+$，求权重最小的生成树。

$E$ 表示边集，$\mathscr{F} = \{F\subseteq E\ |\ F$ 是无圈子图 $\}$，最小生成树问题是求权重最小的极大独立集。（极大独立集就是生成树）

最短路问题：

对于图 $G=(V,E)$，边权 $C:E\rightarrow R^+$，求 s-t​ 的最短路。

$E$ 表示边集，$\mathscr{F} = \{F\subseteq E\ |\ F$ 是一条 s-t 路径的边子集 $\}$，最短路问题是求权重最小的极大独立集。（极大独立集就是一条 s-t 路径）

顶点覆盖问题：

对于无向图 $G=(V,E)$，点权 $C:V\rightarrow R^+$，求权重最小的顶点覆盖（$E$ 中任意一条边的两个顶点至少有一个在）。

$E$ 表示点集，$\mathscr{F} = \{F\subseteq E\ |\ F$ 是某个极小顶点覆盖的子集 $\}$，求权重最大的独立集。

最大权匹配问题：

对于无向图 $G=(V,E)$，边权 $C:E\rightarrow R^+$，求权重最大的边集，其任意两边无公共顶点。

$E$ 表示边集，$\mathscr{F} = \{F\subseteq E\ |\ F$ 中的边无公共顶点 $\}$，求权重最大的独立集。

装箱问题：

对于物品集合，每个物品有相应体积，若干单位容量的箱子，求箱子用量最小的装箱方式。

设单个箱子的可行装填方案有 $M$ 个，用 $t_i$ 表示一个单箱装填方案，则任一个装箱的可行解都是若干单箱方案的集合，使得每个物品一定出现在某个方案中。

则 $E=\{t_1, ...,t_M\}$，每个方案的权重 $C(t_i) = 1$，$\mathscr{F} = \{F\subseteq E\ |\ F$ 是某个装箱可行解的子集 $\}$，求权重最小的极大独立集。（极大独立集就是一个装箱可行解）

背包问题：

对于物品集合 $E$，每个物品的体积 $C:E\rightarrow R^+$，背包体积给定为 $K$，求权重最大的装包方案。

$E$ 表示物品集合，$\mathscr{F} = \{F\subseteq E\ |\ C(F) \le K$ $\}$，求权重最大的独立集。

旅行商问题：

对于无向图 $G=(V,E)$，边权 $C:E\rightarrow R^+$，求权重最小的哈密尔顿圈。

$E$ 表示边集，$\mathscr{F} = \{F\subseteq E\ |\ F$ 是某个哈密尔顿圈的子集 $\}$，求权重最小的极大独立集。（极大独立集就是哈密尔顿圈）

贪心算法

对于 $(E,\mathscr{F},C)$ 上极大化问题的贪心算法，有 Best in 和 Worst out 两种

Best in：

对权重进行排序： $c_1 \ge c_2\ge ... \ge c_n$

$F = \phi$
for $i$ = 1 to n
if $F\cup e_{i} \in \mathscr{F}$
$F := F\cup e_{i}$

Worst out:

对权重进行排序：$c_1 \ge c_2\ge ... \ge c_n$

$F=E$
for $i$ = 1 to n
if $F\backslash{e_i}$ 含基
$F := F\backslash{e_i}$

• 证明使用Best-in求解极大化问题满足$q(E,F) \leq \frac{G(E,F,c)}{OPT(E,F,C)} \leq 1$，注意下界是与权$c$无关的。

  证明：

  $E_j = \{e_1, e_2, ..., e_ j\}$ C: $E\rightarrow R^+ ,\quad c_1 \ge c_2\ge ...\ge c_n$
  贪心算法解：$G_n,\quad G_j = G_n\cap E_j,\ j = 1,2,...,n$
  最优解：$O_n,\quad O_j = O_n\cap E_j,\ j = 1,2,...,n$
  $\begin{aligned} C(G_n) &= \sum^n_{j=1} (|G_j|-|G_{j-1}|)c_j \\ &= \sum^n_{j=1} |G_j|(c_j-c_{j+1})\\ &\ge \sum^n_{j=1} \rho(E_j)(c_j-c_{j+1}) \quad[G_j是E_j的⼀个极大独立集]\\ &\ge q \sum^n_{j=1} r(E_j) (c_j-c_{j+1}) \quad[ q(E,\mathscr{F}) = \min_{F\subseteq E}\frac{\rho(F)}{\gamma(F)}]\\ &\ge q \sum^n_{j=1} |O_j| (c_j-c_{j+1}) \quad[ \gamma(F) = \max\{|Y|, Y\subseteq F, Y\in \mathscr{F}\} ]\\ &= q\ C(O_n)​ \end{aligned}$

  证下界是紧的：

  由秩商的定义， $\exists F, \frac{\rho(F)}{\gamma(F)} = q(E,\mathscr{F})$，即 $\exists F$ , $F$ 的基 $B_1, B_2$ 满足 $\frac{\vert B_1\vert}{\vert B_2\vert} = q(E, \mathscr{F})$

  定义权重：$c(e) = 1, e\in F;\ c(e) = 0, e\notin F$ 。把 $B_1$ 的元素排在前面 $e_1, e_2, ..., e_{\vert B_1\vert},...$ 。使用Best in，会选择前 $\vert B_1\vert$ 个元素，而最优解可以选 $\vert B_2\vert$ 个元素。

  因此贪心算法的近似比

  $q(E,\mathscr{F}) \le \frac{G(E,\mathscr{F},C)}{OPT(E,\mathscr{F},C)} \le 1$

• Worst out类似：Worst-out求解极小化问题，将元素按照权重从大到小排序，依次尝试去掉一个元素，如果还有一个基剩余那么就去掉该元素，满足$1 \leq \frac{G(E,F,c)}{OPT(E,F,c)} \leq \max_{X \subseteq E}\frac{|X|-\rho*(X)}{|X|-r*(X)}$，其中$X$是$E$的一个任意非独立子集，证明在对偶系统部分。

考虑下面两个问题：极小覆盖集的最大权问题，极大独立集的最小权问题，可以发现只有在best-in用在极大化问题，worst-out用在极小化问题时才可以保证上述两个约束，当然特例是拟阵，两个算法相同

对偶独立系统

定义：
$(E,\mathscr{F}) \rightarrow (E,\mathscr{F}^*)\\\mathscr{F}^* = \{X\subseteq E\ \vert\ \exists\mathscr{F}的一个基B，满足 X\cap B = \emptyset \}$

性质：

• $(E,\mathscr{F}^*)$ 是一个独立集系统：证明满足独立集系统的定义即可

• $B$ 是 $(E,\mathscr{F})$ 的基， 当且仅当， $E\backslash B$ 是 $(E,\mathscr{F}^*)$ 的基：
  若 $A$ 是 $(E,\mathscr{F}^*)$ 的一个基，则 $\exists B\in \mathscr{F},A\cap B = \emptyset$并且B是基
  由于 $A$ 是极大独立集， 再加任何一个就不是独立集，$A = E\backslash B$

• $(E,\mathscr{F}^{**}) = (E,\mathscr{F})$

  $\begin{aligned} \forall X\in \mathscr{F}^{**} &\Leftrightarrow \exists (E,\mathscr{F}^*)的一个基 B^*, X\cap B^* = \emptyset\\ &\Leftrightarrow \exists (E,\mathscr{F})的一个基 B, X\cap (E\backslash B) = \emptyset\\ &\Leftrightarrow \exists (E,\mathscr{F})的一个基 B, X\subseteq B, X\subseteq\mathscr{F} \end{aligned}$

独立集系统的对偶主要用于分析Worst out极小化问题，可以证明：

$1\le \frac{G(E,\mathscr{F},C)}{OPT(E,\mathscr{F},C)} \le \max_{F\neq \emptyset }\frac{\vert F\vert-\rho^*(F)}{\vert F\vert-\gamma^*(F)}$

证明与极大化问题类似.

$G_{j} \cup (E \setminus E_{j})$含有$E$的基，并且任取$e \in G_{j}$，$G_{j} \cup (E \setminus E_{j}) \setminus \{e\}$就不再是$E$的基。

$E \setminus (G_{J} \cup (E \setminus E_{j}))=E_{j} \setminus G_{j}$是$F^{*}$在$E_{j}$上的基，因此$|E_{j}|-|G_{j}| \geq \rho^{*}(E_{j})$。

考虑$O_{n} \subseteq E \setminus (E_{j} \setminus O_{j})$且是一个基，所以$E_{j} \setminus O_{j} \in F^{*}$，因此$|E_{j}|-|O_{j}| \leq r^{*}(E_{j})$ 。

因此我们得到了$\begin{aligned} |G_{j}| \leq |E_{j}|-\rho^{*}(E_{j}) \\ |O_{j}| \geq |E_{j}|-r^{*}(E_{j}) \end{aligned}$，那么令$\lambda = max_{X \subseteq E}\frac{|X|-\rho^{*}(X)}{|X|-r^{*}(X)}$，则有$|G_{j}| \leq \lambda |O_{j}|$，带入best-in证明即可。

秩商的估计式

如果对任意$A \in \mathscr{F}, \ e \in E$，$A + e$最多$P$个圈，则$q(E, \mathscr{F}) \ge 1/p$。

拟阵

拟阵是一类特殊的独立集系统: $(E,\mathscr{F})$ 满足:

• (M1): $\emptyset \in \mathscr{F}$
• (M2): 若 $X\in \mathscr{F},\ \forall Y\subseteq X,Y\in\mathscr{F}$
• (M3): $若X, Y\in\mathscr{F},\vert X \vert >\vert Y\vert ,则 \exists e\in X\backslash Y, Y\cup \{e\}\in\mathscr{F}$ , 也就是说 $Y$ 可从$X$扩充
  (M3’): $若X, Y\in\mathscr{F},\vert X \vert = \vert Y\vert +1,则 \exists e\in X\backslash Y, Y\cup \{e\}\in\mathscr{F}$, 也就是说 $Y$ 可从$X$扩充
  (M3"): $\forall F \subseteq E$, $F$ 上的任何基有相同的元素个数 (要注意这里不只是 $E$ 上的基，而是 $E$ 的任意子集上的基)
  M3, M3’, M3" 是相互等价的，只要满足其中之一的独立集系统就是拟阵。

例子:

1. 向量
   $E = \{v_1,v_2,...,v_m\},\ \mathscr{F} = \{Z\subseteq E\vert Z 是线性无关组\}$

2. 相同的模
   E 是有限集合，K 是一个给定的正整数, $\mathscr{F} = \{X\subseteq E\vert\ \vert X\vert\le K\}$

3. 图拟阵
   $E$ 是无向图 $G$ 中的边集, $\mathscr{F} = \{X\subseteq E, X 构成一个森林\}$

可以看到很多常见的体系都是一个拟阵，如矩阵与线性无关的概念，森林与树。又或者说，拟阵是这些体系的一个抽象，从而分析它们的共性。

拟阵与贪心算法

可以简单得到，拟阵的秩商是 1，根据前面独立集系统的分析，贪心算法的近似比为1。因此，在拟阵中使用贪心算法可以得到最优解。[ 所以最小生成树问题贪心就可以得到最优解。]

用秩商分析得到这个结论是显然的，下面用另一种方法证明拟阵上贪心算法可以得到最优解（来自算法导论）

引理1： (拟阵具有贪心选择性质) 假定 $M= ( S , I )$ 是一个加权拟阵，加权函数为 $ w$ , 且
$S$ 已按权重单调递减顺序排序． 令 $x$ 是S 中第一个满足 $\{x\}$ 独立的元素（ 如果存在）。如果存在这样的 $x$ ， 那么存在 $S$ 的一个最优子集 $A$ 包含$x$．

证明：

1. 如果不存在这样的 $x$ ， 唯一的独立子集是空集，引理显然成立。否则，令B 为任意非
   空最优子集． 假定 $x\notin B$。
2. $B$ 中元素的权重都不大于 $w( x )$: 我们观察到 $y\in B$ 意味 ${y} $是独立的，$x$ 是第一个形成独立集的元素，因此对任意 $y\in B$, 有 $w(x) \ge w(y) $。
3. 构造集合 $A$ . 以 $A = \{x\}$ 开始，集合 $A$ 是独立的。根据 (M3): 若$X, Y\in\mathscr{F}$, $\vert X \vert >\vert Y\vert$, 则$\exists e\in X\backslash Y$,$Y\cup \{e\}\in\mathscr{F}$， 反复寻找 $B$ 中一个可以加入 $A$ 中的新元素, 同时保持 $A$ 的独立性，直至 $\vert A \vert =\vert B\vert$ . 此时， A 和B 的区别仅在 $A$ 包含 $x$ ，而 $B$ 包含另一个元素 $y$ . 由于 $w(x)\ge w(y)$ ,所以 $w(A) = w(B) - w(y) +w(x) \ge w(B)$ 。
4. 由于集合B 是最优的，因此集合A 必然也是最优的，且包含 $x$。

引理2: $M= (S , I )$ 是一个拟阵． 如果 $x$ 是 $S$ 中一个元素， 且它不是 $\emptyset$ 的一个扩展．
那么它也不是 $S$ 的任何独立子集 $A$ 的扩展．

证明：由独立集的定义，独立集中的任何元素 $x$ 自身形成的集合 $\{x\}$ 也是一个独立集。因此若 $\{x\}$ 不是独立集，则 $A\cup\{x\}$ 也不是独立集。

引理2表明， 任何元素如果首次不能用于构造独立集，则之后也不可能被用到。因此，贪心算法跳过 $S$ 中那些不是 $\emptyset$ 的扩展的起始元素，不会导致错误结果。

引理3: （拟阵具有最优子结构性质） $M= (S , I )$ 是一个加权拟阵，$x$ 是 $S$ 中第一个被贪心算法选出的元素，则接下来寻找一个包含 $x$ 的最大权重独立子集的问题归结为寻找加权拟阵 $M'=(S',I')$ 的一个最大权重独立子集的问题， 其中

$S' = \{y\in S:(x,y)\in I\}\\ I' = \{B\subseteq S-\{x\}:B\cup\{x\}\in I\}\\$

$M'$ 的权重函数就是 $M$ 的权重函数，但只局限于S’ 中元素． 我们称 $M'$ 为 $M$ 在元素 $x$ 上的收缩 ( contraction)

证明: 若 $A$ 是 $M$ 的任意一个包含x 的最大权独立子集，则 $A' = A -\{x\}$ 是 $M'$ 的一个独立子集。同时，任何 $M'$ 的独立子集 $A$ 可生成 $M$ 的独立子集 $A = A'\cup\{x\}$ . 均有 $w(A)=w(A')+w(x)$.因此 $M$ 的包含 $x$ 的最大权重独立子集必然生成 $M'$ 的最大权重独立子集．反之亦然．

定理: （拟阵上贪心算法的正确性） 若 $M= ( S , I )$ 是一个加权拟阵，加权函数为 $ w$ ．那么贪心算法返回一个最优子集

证明：由引理2, 贪心算法跳过 $S$ 中那些不是 $\emptyset$ 的扩展的起始元素可永远丢弃． 因为这些元素不会被用到。一旦贪心算法选出第一个元素 $x$， 引理 1 表明算法将 $x$加入 $A$ 不会导致错误结果， 因为必然存在包含 $x$ 的最优子集。 引理 3 说明剩下的问题就是如何寻找拟阵 $M'$ 的最优子集， $M'$ 是 $M$ 在 $x$ 上的收缩。将 $A$ 设为 $\{ x\}$ 后．我们可以将之后的所有步骤解释为拟阵 $M' =(S',I')$上的操作,因为对所有集合 $B\in I'$ , $B$ 在 $M'$ 中独立当且仅当 $B\cup\{x\}$ 在 $M$ 中独立。因此， 贪心算法随后的操作将会找到M’ 的一个最大权重独立子集。而其所有操作的总体效果就是找到 $M$ 的一个最大权重独立子集。

拟阵与独立系统

独立集系统的交： $(E,\mathscr{F}_1), (E,\mathscr{F}_2)$ 的交为 $(E,\mathscr{F}_1\cap\mathscr{F}_2)$

任何一个独立集系统⼀定是有限个拟阵的交。构造法证明：

记独立集系统为 $(E,\mathscr{F})$ , 设独立集系统有 $k$ 个圈： $c_1,c_2,...,c_k$

令 $\mathscr{F}_i = \{X\subseteq E\vert X\nsupseteq c_i\}$ , 可以证明 $(E,\mathscr{F}_i)$ 是一个独立集系统。

[ 这里很容易弄晕，解释一下。前面说过独立集系统表示了一个集合与一个规则，在这里不同的 $\mathscr{F}_i$ 表示了不同的规则，因此形成了不同的独立集系统，每个独立集系统都确定了哪些是独立集哪些不是。 $(E,\mathscr{F}_i)$ 这个独立集系统表示的是：如果一个集合不包含 $c_i$ 中的所有元素，则它是一个独立集。对于第 $i$ 个独立集系统，独立集可以包含其他圈。圈的概念是极小相关集，但这里的相关集是独立集系统 $(E,\mathscr{F})$ 中的相关集，在当前的独立集系统中，包含 ‘圈’ 的集合仍可以是独立集 ]

下证， $(E,\mathscr{F}_i)$ 是拟阵，用 M3": $\forall F \subseteq E$, $F$ 上的任何基有相同的元素个数。对于 $\forall F \subseteq E$

1. $F \nsupseteq c_i$ ，则整个集合 $F$ 是一个独立集，因此它就是 $F$ 上的极大独立集， $F$ 上的基有相同的元素个数
2. $F \supseteq c_i$ ，对 $\forall e\in c_i$ , $F\backslash {e}$ 是极大独立集， $F$ 上的基有相同的元素个数

现证 $\mathscr{F} = \cap_{i = 1}^k \mathscr{F}_i$

• $\mathscr{F} \subseteq \cap_{i = 1}^k \mathscr{F}_i$:
  $\forall X\in \mathscr{F},X$ 不包含任何圈, $X\in\mathscr {F}_i,i=1,...,k \ \Rightarrow X\in \cap_{i = 1}^k \mathscr{F}_i$

• $\mathscr{F} \supseteq \cap_{i = 1}^k \mathscr{F}_i$
  $\forall X\in \mathscr{F}_i,X$不包含圈 $c_i$ 。$\forall X\in\cap_{i = 1}^k \mathscr{F}_i\Rightarrow X$不包含任何圈 $\Rightarrow X\in \mathscr{F}$

[ 需要指出的是，这里只是用构造法说明了任何⼀个独⽴集系统都可以表示为有限个拟阵的交，但用这种构造不一定能分解为最少的拟阵，在实际应用中不一定能得到紧的解 ]

少数的例子：

对于二部图 $G=(A\cup B,E)$, $(E,\mathscr{F})$ 表示图的匹配的独立集系统。

$\mathscr{F}_1 = \{X\subseteq E, \vert\delta _X(u)\vert\le 1,\forall u\in A\}\\ \mathscr{F}_2 = \{Y\subseteq E, \vert\delta _Y(u)\vert\le 1,\forall u\in B\}\\$

其中 $\delta_X(u)$ 表示 $u$ 的度数，只考虑 $X$ 中的边。可以证明， $(E,\mathscr{F}_1),(E,\mathscr{F}_2)$ 是拟阵且 $\mathscr{F} = \mathscr{F}_1\cap \mathscr{F}_2$ 。

若独立集系统是 $k$ 个拟阵的交，则贪心解的近似比至少为 $1/k$

记独⽴集系统为 $(E，\mathscr{F})$，是 $k$ 个拟阵 $(E，\mathscr{F}_i)$ 的交。

证：即证秩商 $q(E ,\mathscr{F}) \ge 1 /k$ 。对 $\forall F\subseteq E$, 考虑 $(E ,\mathscr{F})$ 在 $F$ 上任意两个不同的极⼤独⽴集 $A, B$ $\vert B\vert \ge \vert A\vert$ , 只需证 $\vert B\vert \le k\vert A\vert$

$A_i$ 是 $(E,\mathscr{F}_i)$ 在 $A\cup B$ 上含 $A$ 的极大独立集，容易得 $A = \bigcap_{i=1}^k A_i$
$B_i$ 是 $(E,\mathscr{F}_i)$ 在 $A\cup B$ 上含 $B$ 的极大独立集，$B = \bigcap_{i=1}^k B_i$

$\forall e \in B\backslash A$, ，由于 $e\notin A$, 有 $e\notin \bigcap_{i=1}^k A_i$, 则 $e$ 不可能同时在每个 $A_i$ , $e$ 最多同时出现在 $k-1$ 个 $A_i\backslash A$ 中。每一个 $B\backslash A$ 中的元素最多在 $k-1$ 个 $A_i\backslash A$ 中，因此有 $\frac{1}{k-1}\sum_{i=1}^k \vert A_i\backslash A\vert \le \vert B\backslash A\vert$ , 于是：

$\sum_{i=1}^k \vert A_i\backslash A\vert \le (k-1)\vert B\backslash A\vert \le (k-1)\vert B\vert\\ \sum_{i=1}^k \vert A_i\vert - k\vert A\vert\le (k-1)\vert B\vert$

由于 $(E,\mathscr{F}_i)$ 是拟阵， $A_i, B_i$ 是在 $A\cup B $ 上的基，有 $\forall i,\vert A_i\vert = \vert B_i\vert$ .因此

$k\vert B\vert \le\sum_{i=1}^k\vert B_i\vert \le\sum_{i=1}^k\vert A_i\vert \le k\vert A\vert+ (k-1)\vert B\vert\\ \vert B\vert \le k\vert A\vert$

对 $\forall F\subseteq E$, $F$ 上任意两个不同的极⼤独⽴集$A, B$ 有 $\vert A\vert \le \vert B\vert\le k\vert A\vert$， 因此秩商最小为 $1/k$ ，贪心解的近似比至少为 $1/k$ 。